Anto ingin beli Pizza, tp Anto tidak punya uang . Lalu Anto meminjam uang kepada Budi Rp. 25.000, dan Citra Rp. 25.000 juga. Total uang yg Anto pinjam Rp.50.000. Lalu Anto membeli Pizza yang harganya Rp.47.000 . Jadi masih ada kembalizn Rp.3000.
Nah, untuk mengurangi utang Anto,uang kembalian sebesar Rp.3000 itu Anto pakai untuk membayar utangnya. Untuk Budi Rp.1000, dan untuk Citra Rp.1000 dan Rp.1000 sama Anto . Jadi utang Anto ke Si A jd Rp.24.000 dan ke Si B juag jadi Rp.24.000.
Jika di Jumlahkan,
24+24 = 48rb +1rb (uang yg ada di Anto) = Rp.49.000.!
Jadi YANG Rp.1000 DIMANA??.. Sedangkan jumlah utang Anto total Rp.50.000.
Jawabannya :
pinjam beli pizza kan 47.000, yang di bayarkan baru 2.000, Anto bawa 1.000
47.000 (harga pizza) + 2.000 (yg di bayar ke A dan B ) + 1.000 (dibawa Anto) = 50.000
Ruas kiri = utang Anto
Ruas kanan = uang Anto
25 + 25 = 50
25 + 25 = 3 + 47 (beli pizza)
25 + 25 = 1 + 2 + 47
25 + 25 - 2 = 1 + 47
48 = 1 + 47
47 = 47
Itu artinya Anto cuma pinjem 47rb, 48rb yang Anto maksud itu adalah utang Anto yang belum ditambah uang 1000 yang Anto punya.
Kalo udah di kalkulasi utang Anto 47rb
2. Mempertanyakan Kebenaran Rumus Pasti Matematika
Apakah benar 1 = 1?
X2 = X2
X2 - X2 = X2 - X2 >> dua2nya ditambah -X2 biar sama hasilnya (rumus standar dalam matematika)
X (X - X ) = ( X + X )( X - X ) ingat rumus X2 - Y2 = (X - Y )(X + Y)
X (X - X ) = ( X + X )( X - X )
X = X + X
X = 2 X
1 = 2 (1)
jadi....
1 = 2 Lho?? kok gitu??
Gimana ini??,,
Jawaban :
Bagaimana?
X2 = X2
X2 - X2 = X2 - X2 >> dua2nya ditambah -X2 biar sama hasilnya (rumus standar dalam matematika)
X (X - X ) = ( X + X )( X - X ) ingat rumus X2 - Y2 = (X - Y )(X + Y)
X = X + X
X = 2 X
1 = 2 (1)
jadi....
1 = 2 Lho?? kok gitu??
Gimana ini??,,
Jawaban :
Bagaimana?
Sudah dibaca belum soalnya dengan seksama?
Atau teman-teman menemukan kesimpulan aneh di “cara pengerjaan” nya? Hehe..
memang IYA kawan!
Letak kesalahannya ada pada contoh di atas itu, karena menggunakan sistem coret- mencoret X-X di sisi kiri dan sisi kanan. Padahal hal itu TIDAK BOLEH.. Alasannya?
Begini, di situ ada X-X, kalau ditelaahr, X-X = 0 kan?
Sisi kiri ada X-X, sisi kanan ada X-X juga, trus dicoret!! BOLEH???
JELAS NGGAK BOLEH!! Kenapa?
Kalau X-X = 0, brati sisi kiri dan kanan adalah
X(0) = (0)(X+X)
0 = 0, kalau kita pindah angka 0 yang di kanan ke kiri. Menjadi:
0/0 = 1, BETUL???
SALAH!!!
0 dibagi dengan 0 itu BILANGAN TAK TENTU. Jadi bukan hanya 1. Tapi bisa -…, -2, -1, 0, 1, 2, …,
Bukankah semua bilangan kalau dikalikan 0 akan sama dengan 0? Hehe..
Jadi kesalahan contoh kasus di atas adalah, PELANGGARAN dalam membagi bilangan.
3. Pertanyaan Logika Dalam matematika
si A, B, & C patungan 25 juta untuk beli rumah, jadi hasil patungan A+B+C= 75 juta.
si D sebagai makelar pembelian rumah, sehingga dibelikan rumah seharga 70 juta.
So (A+B+C)-D= 75 juta-70 juta= 5 juta.
sisa uang 5 juta dikembalikan si D kepada A, B, & C masing-masing 1 juta, jadi sisa 2 juta untuk biaya makelar si D. (5 juta- 3 juta= 2 juta).
Secara perhitungan si A, B, & C jumlah patungannya hanyalah 24 juta (25 juta- 1 juta= 24 juta).
Setelah ditotal hasilnya aneh, A+B+C= 24+24+24= 72 juta, sedangkan uang yang diambil sebagai biaya makelar oleh D adalah 2 juta, so A+B+C+D= 24+24+24+2= 74 juta, sedangkan hasil patungan pertama kali adalah 75 juta, coba cari yang 1 juta kemana??? (75 juta-74 juta= 1 juta, kemana???)
Jawaban :
Perhatikan lagi soal kalimat matematika diatas. Kenapa dia menyimpulkan patungannya 24 juta? Perhatikan lagi harga rumahnya berapa, 70 juta!
Kalau 70 juta itu dibagi 3 (A,B dan C), maka patungannya bukan 25 juta lagi, tapi 70/3 = 23,333 juta.
Nah, sisa 5 juta itu dibagikan ke A, B, C masing-masing 1 juta. Jadi patungannya jadi 23,333 + 1 = 24,3333 juta.
Sekarang A+B+C = 24,333 + 24,333 + 24,333 = 73 juta
Duit makelar = 2 juta, jadi 73 juta + 2 juta = 75 juta!
Mana yang “kemana”? Semua baik-baik saja tuh duitnya, gak ada yang ilang… xixixi…
2. Keindahan dari pengolahan angka dalam Matemetika
| Hasil Pengolahan angka 6 |
| 6 x 7 = 42 |
| 66 x 67 = 4422 |
| 666 x 667 = 444222 |
| 6666 x 6667 = 44442222 |
| 66666 x 66667 = 4444422222 |
| 666666 x 666667 = 444444222222 |
| 6666666 x 6666667 = 44444442222222 |
| 66666666 x 66666667 = 4444444422222222 |
| 666666666 x 666666667 = 444444444222222222 |
| Hasil pengolahan angka 9 |
| 9 x 9 = 81 |
| 99 x 99 = 9801 |
| 999 x 999 = 998001 |
| 9999 x 9999 = 99980001 |
| 99999 x 99999 = 9999800001 |
| 999999 x 999999 = 999998000001 |
| 9999999 x 9999999 = 99999980000001 |
| 99999999 x 99999999 = 9999999800000001 |
| 999999999 x 999999999 = 999999998000000001 |
| Hasil pengolahan angka urut tanpa angka 8 |
| 12345679 x 9 = 111111111 |
| 12345679 x 18 = 222222222 |
| 12345679 x 27 = 333333333 |
| 12345679 x 36 = 444444444 |
| 12345679 x 45 = 555555555 |
| 12345679 x 54 = 666666666 |
| 12345679 x 63 = 777777777 |
| 12345679 x 72 = 888888888 |
| 12345679 x 81 = 999999999 |
| Hasil pengolahan angka 8 |
| 1 x 8 + 1 = 9 |
| 12 x 8 + 2 = 98 |
| 123 x 8 + 3 = 987 |
| 1234 x 8 + 4 = 9876 |
| 12345 x 8 + 5 = 98765 |
| 123456 x 8 + 6 = 987654 |
| 1234567 x 8 + 7 = 9876543 |
| 12345678 x 8 + 8 = 98765432 |
| 123456789 x 8 + 9 = 987654321 |
| Hasil Pengolahan angka 1 dan 9 |
| 1 x 9 + 2 = 11 |
| 12 x 9 + 3 = 111 |
| 123 x 9 + 4 = 1111 |
| 1234 x 9 + 5 = 11111 |
| 12345 x 9 + 6 = 111111 |
| 123456 x 9 + 7 = 1111111 |
| 1234567 x 9 + 8 = 11111111 |
| 12345678 x 9 + 9 = 111111111 |
| 123456789 x 9 + 10 = 1111111111 |
4. Keindahan Hasil jawaban siswa yang frustasi terhadap soal matematika dan sejenisnya
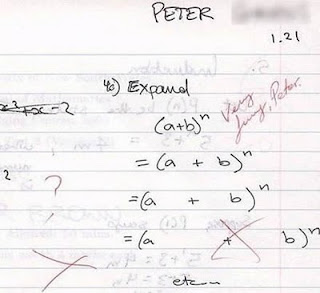







0 komentar:
Posting Komentar